Algebraic Geometry and Linear Logic This thesis develops a geometric model for shallow multiplicative exponential linear logic proofs using Hilbert schemes, interpreting proofs as polynomials that correspond to closed subschemes of projective space. It connects linear logic to algebraic geometry and computational aspects like cut-elimination, exploring links to error-correcting codes, matrix factorizations, and functional programming.
Linear Logic and the Hilbert Scheme Extending an algebraic model of multiplicative linear logic to shallow proofs using the Hilbert scheme.
Linear Logic and Quantum Error Correcting Codes A connection between multiplicative proof nets in linear logic and quantum error-correcting codes is defined, interpreting cut-elimination as a quantum cooling process that reduces a system to its ground state. It formalizes this relationship using stabilizer codes, associating logical transformations with physical quantum operations and introducing examples like Majorana chains.
Elimination and cut-elimination This paper defines a ring associated with a proof net by quotienting a polynomial ring based on formula identifications, linking proof normalization to Gröbner bases via the Buchberger Algorithm. It introduces the Falling Roofs algorithm, an adapted version of Buchberger’s method, to handle cases where the proof net is not in normal form.

The Internal Logic and Topoi Topoi are often described as “generalized theories of sets,” but are they? This description is frequently attributed to topoi due to the similarities between their internal logic and ZF set theory. We examine the differences between topoi and ZF set theory, emphasizing how their internal logics handle unions and products differently. It explores the implications of these differences when translating set-theoretic definitions into the internal language of a topos.
Gentzen-Mints-Zucker Duality We explore the duality between the simply typed λ-calculus and the intuitionistic sequent calculus, highlighting their local and global perspectives on the same structure. It emphasizes how their differences, particularly in cut-elimination and β-equivalence, make the duality both informative and natural.
Simplifying normal functors: an old and a new model of λ-calculus We contrast two approaches to modeling linear logic—one prioritizing categorical models and the other emphasizing syntax through cut-elimination. It simplifies Girard’s normal functors model, introduces a new syntactic perspective, and challenges the necessity of categorical models by emphasizing the inherent linearity of linear logic.
Finite simplicial sets are algorithms In reference to the paper 'the Internal Logic and Topoi', we also implicitly formalise the idea that finite simplicial sets act as algorithms computing their geometric realisations, viewing the internal logic of a topos as a constructive programming language.
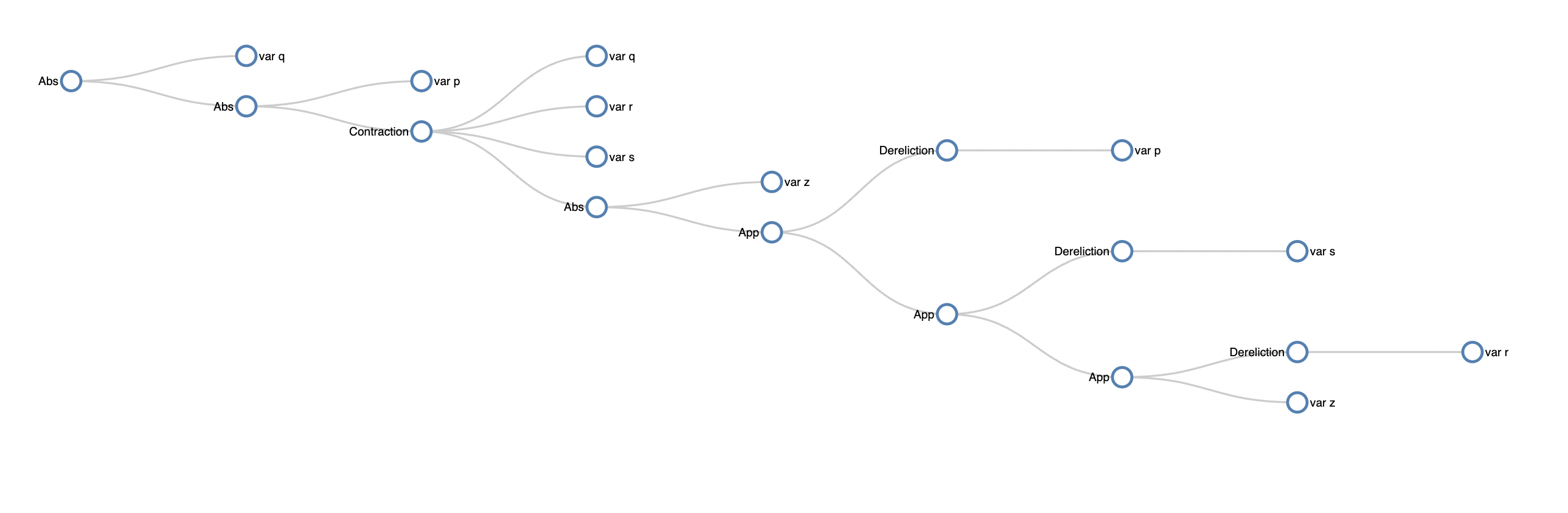
A proof tree constructor for the Linear Lambda Calculus
A parser for the linear λ-calculus, generating HTML representations of unique term-constructing trees.
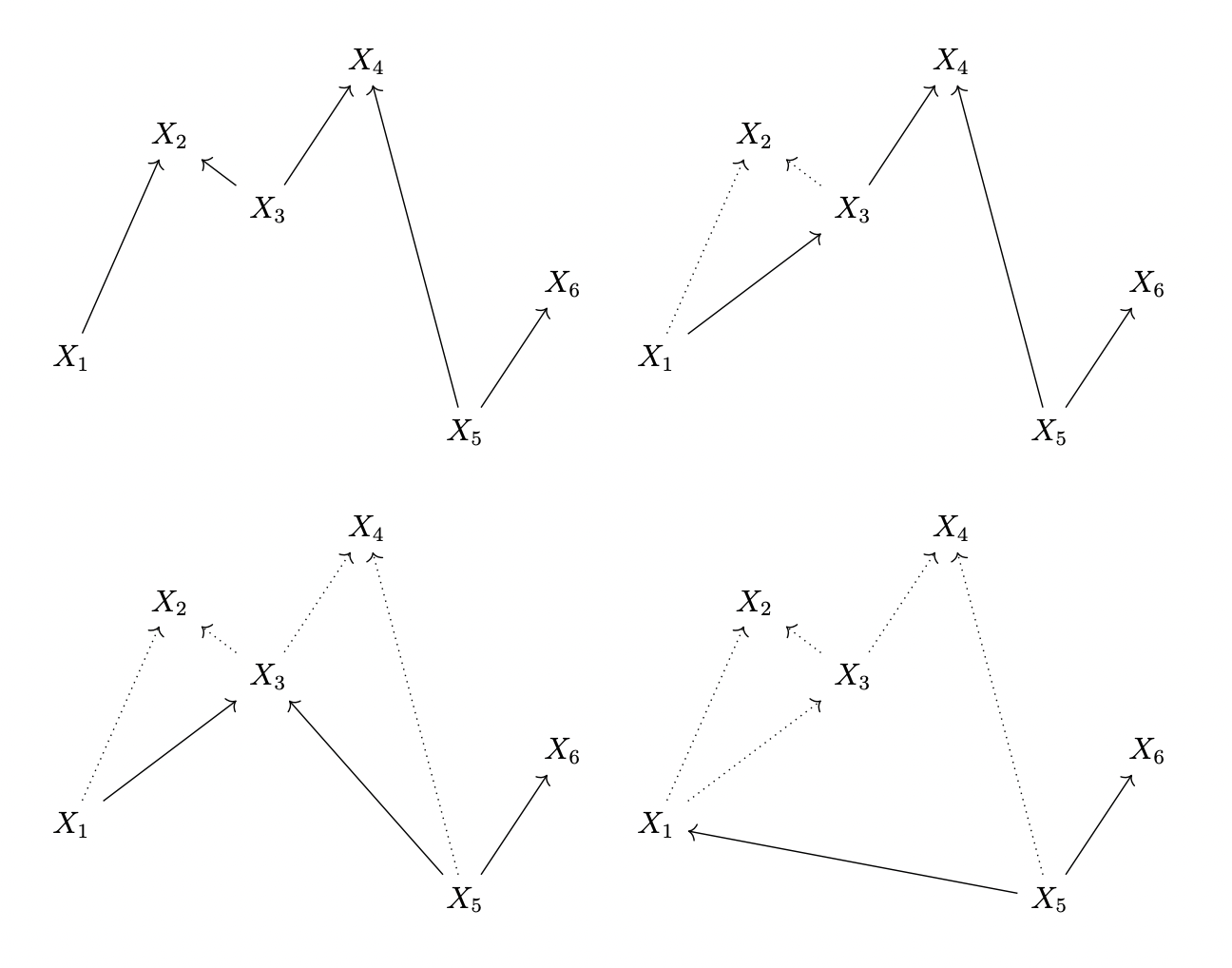
For instance, the term
\( \lambda q \lambda p.\, \texttt{copy } q \texttt{ as } r, s \texttt{ in } \lambda z.\, \texttt{derelict}(p)(\texttt{derelict}(s)(\texttt{derelict}(r)z)) \)
has the following diagram associated with it.
Elementary commutative algebra: Linear algebra, rings and modules, polynomial rings, fields, field extensions, integral extensions and Jacobson rings, dimension theory, discrete valuation rings, completions.
Secondary algebra: Graded rings/modules/algebras, (quasi-)regular sequences, Clifford algebras.
Introduction to varieties: Affine varieties, projective varieties (Gröbner bases), morphisms, singularities.
Introduction to the untyped λ-Calculus: Church-Rosser Theorem.
Introduction to linear logic: multiplicatives: The sequentialisation theorem, geometry of interaction 0 (proofs as permutations), persistent paths, geometry of interaction 1 (proofs as operators).
Gödel's First Incompleteness Theorem: General recursive functions, Chinese Remainder Theorem, β-function, diagonalisation, Gödel's sentence.
First order logic: Syntax, semantics, proof (natural deduction), Skolemisation, Lowenhiem-Skolem Theorem, Compactness Theorem.
The Ax-Grothendieck Theorem: Transporting proofs, algebraic completeness.
A mathematician's introduction to quantum error correction: Quantum computing, the density operator, error correction (examples), general error correction, stabilisers.
Reversible computation: "Reverse" of a Turing Machine, Turing Machines are reversible.
Approximation of Continuous Functions by ReLU Nets: Feed-forward ReLU activations, approximation by polynomials.
Some of the following seminars took place at metauni, a virtual and free-to-access campus. Come and join us on discord
A philosophical journey through mathematics and music
Computation in logic as the splitting of idempotents in algebraic geometry; two models of multiplicative linear logic (repeat of ChoCoLa talk, slides are different)
Normal functors[ions], [the irrelevance of] power series, and [a new model of] λ-calculus
Computation in logic as the splitting of idempotents in algebraic geometry; two models of multiplicative linear logic slides
Story telling (in mathematics and music) video notes synopsis/transcript
An object is whole only with its contrary; composing music and creating mathematics video synopsis/transcript
Quantum error correcting codes and cut-elimination video (scroll down)
First order logic video
Models of first order theories video
Gödel's First Incompleteness Theorem Part 1 (proof sketch) video
Gödel's First Incompleteness Theorem Part 2 (general recursive functions) video
Gödel's First Incompleteness Theorem Part 3 (Chinese Remainder Theorem and the β-function trick) video
Gödel's First Incompleteness Theorem Part 4 (properties of general recursive functions) video
Gödel's First Incompleteness Theorem Part 5 (general recursive functions are representable 1) video
Gödel's First Incompleteness Theorem Part 6 (general recursive functions are representable 2) video
Ax–Grothendieck Theorem part 1 (proof sketch) video
Ax–Grothendieck Theorem part 2 (the geometric part) video
Ax–Grothendieck Theorem part 3 (Skolemisation) video
Ax–Grothendieck Theorem part 4 (Lower Lownehiem-Skolem Theorem) video
Ax-Grothendieck Theorem part 5 (Finishing the proof) video
Introduction to Category Theory
Topoi and logic 1
Topoi and logic 2
Elimination and cut-elimination
Proofs, rings, and ideals, slides
Proof nets video
The Sequentialisation Theorem video
Geometry of Interaction Zero, proofs as permutations video
Gentzen-Mints-Zucker Duality, video
Reversible Turing Machines, notes
A crash course in simplicial cohomology with coefficients in Z mod 2, notes
Arithmetisation and localisation, notes
Approximation of Continuous Functions by ReLU Nets, notes
Monads and programs, notes
Higher-order Logic and Topoi, notes
The Classifying Space of Rings, notes
Monads and Programs, slides
The Church-Rosser Theorem, notes, improved notes
Introduction to Lambda-Calculus, notes
System F in the real world: Haskell and functional programming, notes, the referenced talk by Rich Hickey is Simple made easy
Nobby's statement:
Nature (in the form of gravity and as a commanding higher voice) has had its say; now for a more rigorous formal approach.
Using the integer 1 and the first four prime numbers, 2, 3, 5 and 7, I constructed a Cartesian grid centred on x and y = 0. I plotted all possible positive and negative values of the x and y coordinates (48 in all) and these formed the vertices of a square grid. Then I selected the 24 outmost coordinates and these served as the centrepoint of circles whose circumference passed through the midpoint of the previously established grid squares. This formed an interlocking path of arc quadrants which form the (blue) trajectory above, reminiscent of patterns in in early Chinese and Islamic Design. The central void also appealed to me, for reasons at this stage unfathomable.
I was pleased to see the frame as a trajectory, emerging from the geometric matrix that shapes much of our world.
There is a famous optical illusion in which some people see a duck, others a rabbit. My friend Will Troiani, who has tutored me over the years in mathematics I have required for various projects, turns up at the studio, looks at my Trajectory and sees a beautiful algorithm lurking there.
Before we reach the concluding work, Taming the Frame, I am delighted by any confluence of visual theory and science, Take it away Will.
